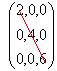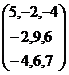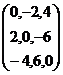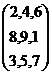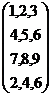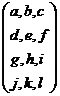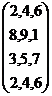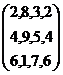3.5 ªÀiÁvÀÈPÉUÀ¼À «zsÀUÀ¼ÀÄ(Types of Matrices):

ªÁåSÉåUÀ¼ÀÄ:

MAzÀÄ ªÀUÀð ªÀiÁvÀÈPÉ(‘Square Matrix’ )AiÀÄ°è CqÀظÁ®ÄUÀ¼ÀÄ ªÀÄvÀÄÛ PÀA§¸Á®ÄUÀ¼À ¸ÀASÉå ¸ÀªÀĪÁVgÀÄvÀÛzÉ. ªÀUÀð ªÀiÁvÀÈPÉAiÀÄ ±ÉæÃtÂ(order): (m x m)
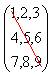
A= ±ÉæÃt :3X3 B= ±ÉæÃt : 2X2	ªÀiÁvÀÈPÉ A AiÀÄ°è ¥ÀæzsÁ£À PÀtðzÀ(‘Diagonal’) CA±ÀUÀ¼ÀÄ {1,5,9}(JqÀªÉÄîÄÛ¢¬ÄAzÀ §® PɼÀvÀÄ¢AiÀĪÀgÉUÉ) ªÀiÁvÀÈPÉ B AiÀÄ°è ¥ÀæzsÁ£À PÀtðzÀ(‘Diagonal’) CA±ÀUÀ¼ÀÄ {1,4}(JqÀªÉÄîÄÛ¢¬ÄAzÀ §® PɼÀvÀÄ¢AiÀĪÀgÉUÉ)
A= B=	ªÀiÁvÀÈPÉ A 3X2 ªÀÄvÀÄÛ ªÀiÁvÀÈPÉ B 2X3 ±ÉæÃtÂAiÀÄ ªÀiÁvÀÈPÉUÀ¼À£ÀÄß UÀªÀĤ¹. EªÉgÀqÀÆ ªÀUÀð ªÀiÁvÀÈPÉUÀ¼À®è. DzÀÝjAzÀ EªÀÅUÀ¼À°è ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ½®è.
MAzÀÄ ªÀUÀð ªÀiÁvÀÈPÉAiÀÄ°è ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼À£ÀÄß ©lÄÖ G½zɯÁè CA±ÀUÀ¼ÀÄ ¸ÉÆ£ÉßAiÀiÁVzÀÝgÉ CzÀÄ PÀtð ªÀiÁvÀÈPÉ(‘Diagonal matrix’).
A=¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {2,4,6} B= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {3,6}	A ªÀÄvÀÄÛ B ªÀiÁvÀÈPÉUÀ¼À°è ¥ÀæzsÁ£À PÀtðzÀ CA±ÀUÀ¼À£ÀÄß ©lÄÖ G½zɯÁè CA±ÀUÀ¼ÀÄ ¸ÉÆ£Éß.
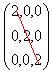
¥ÀæzsÁ£À PÀtðzÀ CA±ÀUÀ¼É®èªÀÇ ¸ÀªÀĪÁVgÀĪÀ PÀtðªÀiÁvÀÈPÉAiÀÄÄ MAzÀÄ ¥ÀjªÀiÁt ªÀiÁvÀÈPÉ(‘Scalar matrix’).
A= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {2,2,2 B= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {5,5}
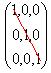
MAzÀÄ PÀtðªÀiÁvÀÈPÉAiÀÄ PÀtðzÀ CA±ÀªÀÇ 1 PÉÌ ¸ÀªÀĪÁVzÀÝgÉ CzÀÄ WÀlPÀ ªÀiÁvÀÈPÉ CxÀªÁ C£À£Àå ªÀiÁvÀÈPÉ(‘Identity matrix’)
A= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {1,1,1} B= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {1,1}
¥ÀæzsÁ£À PÀtðPÉÌ ¸ÀªÀÄ«ÄwAiÀÄ£ÀÄß ºÉÆA¢zÀ CA±ÀUÀ¼ÀÄ ¸ÀªÀĪÁVgÀĪÀ MAzÀÄ ªÀUÀðªÀiÁvÀÈPÉAiÀÄ£ÀÄß ¸ÀªÀÄ«Äw ªÀiÁvÀÈPÉ (‘Symmetric matrix’) J£ÀÄߪÀgÀÄ.
A=¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {5,9,7} B= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {7, 9}	A £À ¥ÀæzsÁ£À PÀtðzÀ JgÀqÀÆ §¢UÀ¼À°ègÀĪÀ CA±ÀUÀ¼ÀÄ MAzÉÃ: {-2,-2},{-4,-4},{6,6} B £À ¥ÀæzsÁ£À PÀtðzÀ JgÀqÀÆ §¢UÀ¼À°ègÀĪÀ CA±ÀUÀ¼ÀÄ MAzÉÃ: {-2,-2}.
¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼É¯Áè ¸ÉÆ£ÉßAiÀiÁVzÀÄÝ, ¥ÀæzsÁ£À PÀtðPÉÌ ¸ÀªÀÄ«Äw ºÉÆA¢gÀĪÀ CA±ÀUÀ¼ÀÄ ¸ÀªÀĪÁVzÀÄÝ, aºÉßUÀ¼À°è «gÀÄzÀÞªÁVgÀĪÀ MAzÀÄ ªÀUÀð ªÀiÁvÀÈPÉAiÀÄ£ÀÄß «µÀªÀÄ ¸ÀªÀÄ«Äw ªÀiÁvÀÈPÉ (‘Skew symmetric matrix’ ) J£ÀÄߪÀgÀÄ.
A=¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {0,0,0} B= ¥ÀæzsÁ£À PÀuÁðA±ÀUÀ¼ÀÄ: {0,0}	A £À ¥ÀæzsÁ£À PÀtðzÀ JgÀqÀÆ §¢UÀ¼À°ègÀĪÀ CA±ÀUÀ¼ÀÄ MAzÉà DVzÀÄÝ «gÀÄzÀÞ aºÉßUÀ¼À£ÀÄß ºÉÆA¢ªÉ: {-2,2},{4,-4},{-6,6} B £À ¥ÀæzsÁ£À PÀtðzÀ JgÀqÀÆ §¢UÀ¼À°ègÀĪÀ CA±ÀUÀ¼ÀÄ MAzÉà DVzÀÄÝ «gÀÄzÀÞ aºÉßUÀ¼À£ÀÄß ºÉÆA¢ªÉ: {-2,2}.)
A= ±ÉæÃtÂ: 1X4 B= ±ÉæÃtÂ: 1X2	MAzÀÄ ªÀiÁvÀÈPÉAiÀÄÄ PÉêÀ® MAzÀÄ CqÀØ ¸Á®£ÀÄß ºÉÆA¢zÀÝgÉ. CzÀÄ CqÀظÁ®Ä ªÀiÁvÀÈPÉ (‘Row matrix’). CqÀظÁ®Ä ªÀiÁvÀÈPÉAiÀÄ ±ÉæÃtÂ: (1 x n).
A= ±ÉæÃtÂ: 4X1 B= ±ÉæÃtÂ: 2X1	MAzÀÄ ªÀiÁvÀÈPÉAiÀÄÄ PÉêÀ® MAzÀÄ PÀA§ ¸Á®£ÀÄß ºÉÆA¢zÀÝgÉ. CzÀÄ PÀA§¸Á®Ä ªÀiÁvÀÈPÉ (‘Column matrix’). PÀA§¸Á®Ä ªÀiÁvÀÈPÉAiÀÄ ±ÉæÃtÂ:(m x 1)
A= ±ÉæÃtÂ: 3X4 B= ±ÉæÃtÂ: 2X3	MAzÀÄ ªÀiÁvÀÈPÉAiÀÄ J¯Áè CA±ÀUÀ¼ÀÆ ¸ÉÆ£ÉßAiÀiÁVzÀÝgÉ, CAvÀºÀ ªÀiÁvÀÈPÉAiÀÄ£ÀÄß “±ÀÆ£Àå ªÀiÁvÀÈPÉ” (‘Zero matrix’) J£ÀÄߪÀgÀÄ. (±ÀÆ£Àå ªÀiÁvÀÈPÉAiÀÄÄ ªÀUÀð ªÀiÁvÀÈPÉAiÀÄÆ DVgÀ§ºÀÄzÀÄ, DAiÀÄvÀ ªÀiÁvÀÈPÉAiÀÄÆ DVgÀ§ºÀÄzÀÄ.)

A= B= DzÀgÉ, A=B	JgÀqÀÄ ªÀiÁvÀÈPÉUÀ¼ÀÄ MAzÉà ±ÉæÃtÂAiÀÄļÀîªÀÅUÀ¼ÁVzÀÄÝ, MAzÀÄ ªÀiÁvÀÈPÉAiÀÄ ¥ÀæwAiÉÆAzÀÄ CA±ÀªÀÇ JgÀqÀ£Éà ªÀiÁvÀÈPÉAiÀÄ C£ÀÄgÀÆ¥À CA±ÀPÉÌ ¸ÀªÀĪÁVzÀÝgÉ, D JgÀqÀÄ ªÀiÁvÀÈPÉUÀ¼ÀÄ ¸ÀªÀÄ.
A= B = DVzÀÄÝ A=B DzÀgÉ	a=1, b=2,c=3,d=4,e=5,f=6,g=7,h=8,i=9,j=2,k=4,l=6.
ªÀiÁvÀÈPÉAiÀÄ ¸ÀÞ¼ÁAvÀgÀ: MAzÀÄ ªÀiÁvÀÈPÉAiÀÄ°è£À CqÀظÁ®ÄUÀ¼À£ÀÄß PÀA§¸Á®ÄUÀ¼À£ÁßVAiÀÄÆ, PÀA§¸Á®ÄUÀ¼À£ÀÄß CqÀظÁ®ÄUÀ¼À£ÁßVAiÀÄÆ §gÉzÀgÉ zÉÆgÉAiÀÄĪÀ ªÀiÁvÀÈPÉAiÉÄà ªÉÆzÀ°£À ªÀiÁvÀÈPÉAiÀÄ ¸ÀÞ¼ÁAvÀj¹zÀ ªÀiÁvÀÈPÉ(‘Transpose of a matrix’) . A ªÀiÁvÀÈPÉAiÀÄ ¸ÀÞ¼ÁAvÀj¹zÀ ªÀiÁvÀÈPÉAiÀÄ£ÀÄß A^1JAzÀÄ ¸ÀÆa¸ÀÄvÉÛêÉ.
A= F ªÀiÁvÀÈPÉAiÀÄ ±ÉæÃtÂ: 4X3 A^1= ±ÉæÃtÂ: 3X4	CqÀØ ¸Á®ÄUÀ¼ÀÄ: {2,4,6},{8,9,1},{3,5,7},{2,4,6}.PÀA§ ¸Á®ÄUÀ¼ÀÄ: {2,8,3,2},{4,9,5,4},{6,1,7,6} CqÀØ ¸Á®ÄUÀ¼ÀÄ: {2,8,3,2},{4,9,5,4},{6,1,7,6}. PÀA§ ¸Á®ÄUÀ¼ÀÄ: {2,4,6},{8,9,1},{3,5,7},{2,4,6}

3.5 PÀ°vÀ ªÀÄÄSÁåA±ÀUÀ¼ÀÄ

PÀæ.¸ÀA.	ªÀÄÄSÁåA±ÀUÀ¼ÀÄ
1	ªÀiÁvÀÈPÉUÀ¼À «zsÀUÀ¼ÀÄ: ªÀUÀðªÀiÁvÀÈPÉ, DAiÀÄvÀ ªÀiÁvÀÈPÉ, PÀtð ªÀiÁvÀÈPÉ, ¥ÀjªÀiÁt ªÀiÁvÀÈPÉ, C£À£Àå ªÀiÁvÀÈPÉ, ¸ÀªÀÄ«Äw ªÀiÁvÀÈPÉ, «µÀªÀÄ ¸ÀªÀÄ«Äw ªÀiÁvÀÈPÉ, ±ÀÆ£Àå ªÀiÁvÀÈPÉ.
2	ªÀiÁvÀÈPÉUÀ¼À£ÀÄß ¸ÀÞ¼ÁAvÀj¸ÀĪÀÅzÀÄ.