5.5 ಮಾನಕ ವಿಚಲನೆ (Standard Deviation):

ಪೀಠಿಕೆ:  

ನೀವು ವಾರ್ತಾಪತ್ರಿಕೆಗಳಲ್ಲಿ ಇಬ್ಬರು ಕ್ರಿಕೆಟ್ ಆಟಗಾರರ ಆಟದ ತುಲನೆ ಮಾಡುವುದನ್ನು ಓದಿರಬಹುದು. ಅವರು ಏನನ್ನು ತುಲನೆ ಮಾಡುತ್ತಾರೆ? ಒಬ್ಬನು ಇನ್ನೊಬ್ಬನಿಗಿಂತ ಸ್ಥಿರವಾಗಿದ್ದಾನೆ ಅಥವಾ ಒಬ್ಬನು ಇನ್ನೊಬ್ಬನಿಗಿಂತ ಹೆಚ್ಚು ಕಲಾತ್ಮಕವಾಗಿ ಆಡುತ್ತಾನೆ ಎನ್ನುತ್ತಾರೆ. ಕಲಾತ್ಮಕತೆ ಎಂಬುದು ಒಂದು ವಿಶಿಷ್ಟಗುಣ ಮತ್ತು ಅದನ್ನು ಹೋಲಿಕೆ ಮಾಡಲು ಕಷ್ಟ. ಆದರೆ ಅವರು ಗಳಿಸಿದ ರನ್ನುಗಳ ಆಧಾರದ ಮೇಲೆ ಅವರ ಸ್ಥಿರತೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತಾರೆ.

ಹಾಗಾದರೆ ಈ ವಿಚಾರದಲ್ಲಿ ಸಂಖ್ಯಾಶಾಸ್ತ್ರವು ಹೇಗೆ ಸಹಾಯಕವಾಗಿದೆ ನೋಡೋಣ

 

ಮಾನಕ ವಿಚಲನೆ (Standard deviation):

ನೀವು ವಿಚಲನೆ ಶಬ್ದಪ್ರಯೋಗವನ್ನು ತಿಳಿದಿರಬಹುದು. (ನಿಯಮದಿಂದ ವಿಚಲನೆ, ಕೆಲಸದಿಂದ ವಿಚಲನೆ, ಫಲಿತಾಂಶದಿಂದ ವಿಚಲನೆ... ಇತ್ಯಾದಿ) ವಿಚಲನೆಯನ್ನು ಯಾವುದೇ ಒಂದು ಸ್ಥಿರ ಮಾನದಂಡಕ್ಕನುಗುಣವಾಗಿ ಲೆಕ್ಕ ಹಾಕುತ್ತೇವೆ.

‘ಮಾನ’ವು ಸಾಮಾನ್ಯವಾಗಿ ದತ್ತಾಂಶಗಳ ‘ಸರಾಸರಿ’ ಆಗಿರುತ್ತದೆ.

5.5 ಉದಾ.1:  ಒಬ್ಬ ಕ್ರಿಕೆಟ್ ಆಟಗಾರನು 6 ಇನ್ನಿಂಗ್ಸ್ ನಲ್ಲಿ ಗಳಿಸಿದ ರನ್ ಗಳು: 48,50,54,46,48,54

 

ವಿಧಾನ:

ಉಪಯೋಗಿಸುವ ಸಂಕೇತಗಳು:

X = ಪ್ರಾಪ್ತಾಂಕಗಳ ಗಣ. (48,50,54,46,48,54)

N = ಪ್ರಾಪ್ತಾಂಕಗಳ ಸಂಖ್ಯೆ (=6)

 = ದತ್ತಾಂಶಗಳ ಸರಾಸರಿ (AM) = ()/N

d = ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆ = X -

ಹಂತ 1: ದತ್ತಾಂಶಗಳ ಸರಾಸರಿ ಕಂಡುಹಿಡಿಯಿರಿ = (48+50+54+46+48+54)/6 = 50

ಹಂತ 2: d (= X-AM) ಮತ್ತು d² ಗಳನ್ನು ಪ್ರತಿ ಮೌಲ್ಯಕ್ಕೂ ಕಂಡುಹಿಡಿಯಿರಿ.

 

ಲೆಕ್ಕಾಚಾರದ ತಃಖ್ತೆ:

 

ಸಂ.	ರನ್ನುಗಳು (X)	ವಿಚಲನೆ (d) = X-	(ವಿಚಲನೆ)2   = d2
1	48	-2	4
2	50	0	0
3	54	4	16
4	46	-4	16
5	48	-2	4
6	54	4	16
	=300	=0	= 56

ಹಂತ 3: ಪ್ರಸರಣ ವಿಚಲನೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕಿ =/ N

ಹಂತ 4: ಮಾನಕ ವಿಚಲನೆ ಲೆಕ್ಕ ಹಾಕಿ: (SD) =  =

ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಗ್ರೀಕ್ ಅಕ್ಷರ  (ರೋ) ದಿಂದ ಸೂಚಿಸುತ್ತೇವೆ.

 

ಮಾನಕ ವಿಚಲನೆ = = = = = 3.05.

 

ವ್ಯಾಖ್ಯೆ: ಮಾನಕ ವಿಚಲನೆಯು(Standard deviation) ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆಗಳ ವರ್ಗಗಳ ಮೊತ್ತದ ಧನಾತ್ಮಕ ವರ್ಗಮೂಲ ಆಗಿರುವುದು.

ವಿವರಣೆ: ಈ ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ ಸುಮಾರಾಗಿ ಆಟಗಾರನು ಗಳಿಸಿದ ರನ್ನುಗಳ ಅಂಕಗಣಿತದ ಸರಾಸರಿ (=50) ಯಿಂದ 3.05 (3 ) ರಷ್ಟು ವಿಚಲನೆ ಹೊಂದುತ್ತವೆ.

 

ಅಂದರೆ ಅರ್ಥ ಮುಂದಿನ ಪಂದ್ಯದಲ್ಲಿ ಆಟಗಾರನು ಸಾಧಾರಣ 47-53 {(50-3)-(50+3)} ರನ್ನುಗಳನ್ನು ಗಳಿಸಬಹುದು.

 

ಗಮನಿಸಿ: ಅಕಸ್ಮಾತ್ ಆಟಗಾರನ ರನ್ನುಗಳು 48,100,50,10,2,80 ಆಗಿದ್ದರೆ, ಅವನ ಸ್ಥಿರತೆಯನ್ನು ಊಹಿಸಲು ಕಷ್ಟ. ಆದರೆ ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ ಅವನ ರನ್ನುಗಳು 50ರ ಸುತ್ತಮುತ್ತ ಇರುವುದರಿಂದ ನಾವು ಮುಂದಿನ ಪಂದ್ಯಗಳಲ್ಲಿ ಅವನು ಗಳಿಸಬಹುದಾದ ರನ್ನುಗಳನ್ನು ಊಹಿಸಬಹುದು.

 

ಸಾಮಾನ್ಯ ಕ್ರಮ:-

 

ಪ್ರಾಪ್ತಾಂಕಗಳು:X = {x_1, x₂ , x_3……….. x_n} ಆಗಿರಲಿ.

N = ಪ್ರಾಪ್ತಾಂಕಗಳ ಸಂಖ್ಯೆ.

 = ಅಂಕಗಣಿತ ಸರಾಸರಿ (AM) = (x₁+x₂ + x₃+…… x_n)/N= / N

ಹಂತ 1: ಪ್ರತೀ ಪ್ರಾಪ್ತಾಂಕಕ್ಕು ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆ ಕಂಡುಹಿಡಿ. (d=X-) ಮತ್ತು ಅದೇ ರೀತಿ d² ವನ್ನು ಕಂಡುಹಿಡಿ.

ಹಂತ 2: ಪ್ರಸರಣ ವಿಚಲನೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕಿ = ()/ N

ಹಂತ 3: ಮಾನಕ ವಿಚಲನೆ (SD) ಲೆಕ್ಕ ಮಾಡಿ.

 SD = =

 

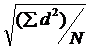
ಪರ್ಯಾಯ ವಿಧಾನ: ಸರಾಸರಿಯು ಪೂರ್ಣಾಂಕವಾಗದೇ ಇರುವಾಗ  ಕಂಡುಹಿಡಿಯುವುದು (Alternate method of finding, when AM is not a whole number):

 

ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ ಸರಾಸರಿಯು ಒಂದು ಪೂರ್ಣಾಂಕವಾಗಿದೆ. ಹಾಗಾಗಿ ಲೆಕ್ಕ ಮಾಡಲು ಸುಲಭವಾಯಿತು. ಆದರೆ, ಅಂಕಗಣಿತದ ಸರಾಸರಿಯು ಒಂದು ಪೂರ್ಣಾಂಕವಾಗದೇ ದಶಮಾಂಶ ಸಂಖ್ಯೆಯಾದಾಗ, d² ವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಕಷ್ಟ. ಅದಕ್ಕಾಗಿ ಇಂತಹ ಸಂದರ್ಭದಲ್ಲಿ ನಾವು ಬೇರೆಯೇ ಕ್ರಮವನ್ನು ಅನುಸರಿಸುತ್ತೇವೆ.

1.      ಯಾವುದಾದರೂ ಒಂದು ಪ್ರಾಪ್ತಾಂಕವನ್ನು ಅಂದಾಜು ಸರಾಸರಿ (A) ಎಂದು ಇಟ್ಟುಕೊಳ್ಳಿ.

2.      ಅಂದಾಜು ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆ D(= X-A) ಗಳನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ.

3.      ವಿಚಲನೆಗಳ ಮೊತ್ತ  ಕಂಡುಹಿಡಿ.

4.      ಪ್ರತಿ ಪ್ರಾಪ್ತಾಂಕದ ವಿಚಲನೆಗಳ ವರ್ಗವನ್ನು ಲೆಕ್ಕಿಸಿ ಮತ್ತು ಈ ವರ್ಗಗಳ ಮೊತ್ತ (d²) ವನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ.

ನೈಜ ಸರಾಸರಿ = ಅಂದಾಜು ಸರಾಸರಿ + ()/N

 

ಮಾನಕ ವಿಚಲನೆ =  [(d²)/N - ((d)/N)²]

 

ಈಗ ನಾವು ಮೇಲೆ ನೋಡಿದ ಉದಾಹರಣೆಯನ್ನೇ ತೆಗೆದುಕೊಂಡು, ಈ ವಿಧಾನದಲ್ಲಿ ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕುವಾ.

ಪ್ರಾಪ್ತಾಂಕಗಳ ಅಂದಾಜು ಸರಾಸರಿ 54 (A = 54.) ಎಂದಿಟ್ಟುಕೊಳ್ಳುವಾ. N = 6.

ಲೆಕ್ಕಾಚಾರದ ತಃಖ್ತೆ

 

ಸಂಖ್ಯೆ	ರನ್ನುಗಳು (X)	ವಿಚಲನೆ (D)  d= X-A	(ವಿಚಲನೆ)2   = d2
1	48	-6	36
2	50	-4	16
3	54	0	0
4	46	-8	64
5	48	-6	36
6	54	0	0
		= -24	= 152

 

ನೈಜ ಸರಾಸರಿ = ಅಂದಾಜು ಸರಾಸರಿ + ()/N= 54 + (-24/6) = 54-4 = 50

 

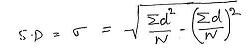
ಮಾನಕ ವಿಚಲನೆ =  [(d²)/N - ((d)/N)²]

 =   [152/6 –(24/6)²] =  (25.33-16) =  (9.33) =3.05

 

ಎರಡೂ ವಿಧಾನಗಳಲ್ಲೂ ಮಾನಕ ವಿಚಲನೆ ಒಂದೇ ಆಗಿದೆ ಎಂದು ಗಮನಿಸಿ.

ಒಂದೇ ಪ್ರಾಪ್ತಾಂಕಗಳು ದತ್ತಾಂಕದಲ್ಲಿ ಹಲವು ಸಾರಿ ಬಂದಿದ್ದರೆ ಈ ಕ್ರಮ ತುಂಬಾ ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಅದಕ್ಕಾಗಿ ಸ್ವಲ್ಪ ಬೇರೆ ವಿಧಾನ ಅನುಸರಿಸುತ್ತೇವೆ.

 

ವರ್ಗೀಕರಿಸಿದ ದತ್ತಾಂಕಗಳಲ್ಲಿ ಮಾನಕ ವಿಚಲನೆ:(Standard Deviation for grouped data):

 

ಒಂದು ವಿತರಣೆಯಲ್ಲಿ ಪ್ರಾಪ್ತಾಂಕಗಳು ಮತ್ತು ಆವೃತ್ತಿಗಳು ಹೀಗಿವೆ:

 

ಮೌಲ್ಯಗಳು (X) ---à	X1	X2	X3	……	Xn
ಆವೃತ್ತಿ (f) ------à	f1	f2	f3	……..	fn

N = ಆವೃತ್ತಿಗಳ ಮೊತ್ತ = f₁ + f₂ + f₃ +…….. f_n=

ಹಂತ 1: ಪ್ರತೀ ಪ್ರಾಪ್ತಾಂಕಕ್ಕೂ  f*x ಕಂಡು ಹಿಡಿಯಿರಿ.

ಹಂತ 2: ಅವುಗಳ ಸರಾಸರಿ ಕಂಡುಹಿಡಿ  = ()/N

ಹಂತ 3: ಪ್ರತಿ ಪ್ರಾಪ್ತಾಂಕಕ್ಕೂ ವಿಚಲನೆ ಕಂಡುಹಿಡಿಯಿರಿ d = (X-)

 

ಹಂತ 4: ಪ್ರಸರಣೆಯ ವಿಚಲನೆ ಕಂಡುಹಿಡಿಯಿರಿ = ((f*d²))/N

 

ಹಂತ 5: ಮಾನಕ ವಿಚಲನೆ ಕಂಡುಹಿಡಿಯಿರಿ: () =  [((f*d²))/N]

 

5.5 ಉದಾ. 2: ಒಂದು ಪರೀಕ್ಷೆಯಲ್ಲಿ 60 ವಿದ್ಯಾರ್ಥಿಗಳು ಗಳಿಸಿದ ಅಂಕಗಳು ಕೆಳಗಿನಂತಿವೆ. ಇವುಗಳಲ್ಲಿ ಮಾನಕ ವಿಚಲನೆ ಕಂಡುಹಿಡಿಯಿರಿ.

 

ಅಂಕಗಳು (X)    ---à	10	20	30	40	50	60
ಆವೃತ್ತಿ(ವಿದ್ಯಾರ್ಥಿಗಳು) (f)--à	8	12	20	10	7	3

 

ವಿಧಾನ:

N (ಆವೃತ್ತಿಗಳ ಮೊತ್ತ)  = = 8+12+20+10+7+3=60

 

ಮೌಲ್ಯಗಳು (X)	ಆವೃತ್ತಿ (f)	fX	ಮೌಲ್ಯಗಳು = d=(X-)	d2	f*d2
10	8	80	-20.83	433.89	3471.11
20	12	240	-10.83	117.29	1407.47
30	20	600	-.83	0.69	13.78
40	10	400	9.17	84.09	840.89
50	7	350	19.17	367.49	2572.42
60	3	180	29.17	850.89	2552.67
	N==60	= 1850			(f*d2)=10858.33

ಸರಾಸರಿ == ()/N= 1850/60 =30.83

ಪ್ರಸರಣ ವಿಚಲನೆ = (f*d²)/N = 10858.33/60= 180.97

ಮಾನಕ ವಿಚಲನೆ: () =  [(f*d²)/N] = (180.97) =13.45

 

ತೀರ್ಮಾನ: ವಿದ್ಯಾರ್ಥಿ ಗಳಿಸಿದ ಅಂಕಗಳ ಸರಾಸರಿ = 30.83. ವಿದ್ಯಾರ್ಥಿಗಳ ಅಂಕಗಳು ಸರಾಸರಿಯಿಂದ 13.45ರಷ್ಟು ವಿಚಲನೆ ಹೊಂದಿರುತ್ತವೆ.

ಈ ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ  ಸರಾಸರಿ ದಶಮಾಂಶ ಸಂಖ್ಯೆಯಾಗಿದೆ. ಆದ್ದರಿಂದಲೇ d, d² ಮತ್ತು f*d² ಗಳು ದಶಮಾಂಶ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದು ಲೆಕ್ಕ ಕಷ್ಟವಾಗಿದೆ ಅದಕ್ಕಾಗಿ, ಇಲ್ಲಿ ಪರ್ಯಾಯ ವಿಧಾನದಿಂದ ಲೆಕ್ಕ ಮಾಡಬೇಕು.

 

 

ಪರ್ಯಾಯ ವಿಧಾನ (Alternate Method)

 

ಹಂತ 1:  ದತ್ತಾಂಶದಲ್ಲಿರುವ ಯಾವುದೇ ಮೌಲ್ಯವನ್ನು ಸರಾಸರಿಯೆಂದಿಟ್ಟುಕೊಳ್ಳಿ (A)

 

ಹಂತ 2: ಪ್ರತೀ ಮೌಲ್ಯಕ್ಕೂ ಈ ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆ (d) ಯನ್ನು ಲೆಕ್ಕ ಹಾಕಿ.

ಹಂತ 3: ಪ್ರತೀ ಮೌಲ್ಯಕ್ಕೂ  f*d, d² ,f*d² ಕಂಡು ಹಿಡಿ.

 

ಹಂತ 4: ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಲೆಕ್ಕ ಹಾಕಿ.

ಸರಾಸರಿ == A + /N, N =

ಮಾನಕ ವಿಚಲನೆ: ()= [(f*d²)/N - ((f*d)/N)² ]

 

ಈಗ ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ 30 ನ್ನು ಅಂದಾಜು ಸರಾಸರಿಯಾಗಿಟ್ಟುಕೊಳ್ಳುವಾ. ಆಗ,

 

ಮೌಲ್ಯಗಳು (X)	ಆವೃತ್ತಿ (f)	ವಿಚಲನೆ (d) =X-A	f*d	d2	f*d2
10	8	-20	-160	400	3200
20	12	-10	-120	100	1200
30	20	0	0	0	0
40	10	10	100	100	1000
50	7	20	140	400	2800
60	3	30	90	900	2700
	N==60		=50		(f*d2)=10900

 

ಸರಾಸರಿ = A+ ()/ (N) = 30+50/60 = 30+0.83= 30.83

 

ಮಾನಕ ವಿಚಲನೆ () =  [(f*d²)/N - ((f*d)/N)²]

=  [(10900/60) – (50/60)²]

=  (181.67 - 0.69) = (180.97) =13.45

 

ವಿದ್ಯಾರ್ಥಿಗಳ ಅಂಕಗಳ ಸರಾಸರಿ = 30.83. ವಿದ್ಯಾರ್ಥಿಗಳ ಅಂಕಗಳು ಸರಾಸರಿಯಿಂದ 13 ಅಂಕಗಳಷ್ಟು ವಿಚಲನೆ ಹೊಂದುತ್ತವೆ.

ಎರಡೂ ವಿಧಾನದಲ್ಲೂ ಒಂದೇ  ಉತ್ತರ ಬಂದಿರುವುದನ್ನು ಗಮನಿಸಿ.

 

ಹೆಚ್ಚಿನ ಸಂದರ್ಭದಲ್ಲಿ ವರ್ಗೀಕರಿಸಿದ ದತ್ತಾಂಶಗಳನ್ನು ಕೊಡುವುದರಿಂದ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಕಂಡು ಹಿಡಿಯಬೇಕಾಗುತ್ತದೆ.

 

ವರ್ಗೀಕೃತ ದತ್ತಾಂಶಗಳಲ್ಲಿ ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಕಂಡು ಹಿಡಿಯುವ ಕ್ರಮ:

 

ಹಂತ 1: ಪ್ರತಿ ವರ್ಗಾಂತರದ ಮಧ್ಯ ಬಿಂದುವನ್ನು ಕಂಡು ಹಿಡಿಯಿರಿ.

ಹಂತ 2: ಪ್ರತೀ ವರ್ಗಾಂತರಕ್ಕು  f*x ಕಂಡು ಹಿಡಿಯಿರಿ.

ಹಂತ 3: ಅಂಕಗಣಿತದ ಸರಾಸರಿ ಕಂಡು ಹಿಡಿಯಿರಿ == ( )/N, N = .

 

ಹಂತ 4: ಪ್ರತಿ ವರ್ಗಾಂತರಕ್ಕೂ ಸರಾಸರಿಯಿಂದ  ()ವಿಚಲನೆ ಕಂಡು ಹಿಡಿಯಿರಿ (d=X-)

 

ಹಂತ 5: ಪ್ರತಿ ವರ್ಗಾಂತರಕ್ಕೂ d²  ಮತ್ತು f*d² ಕಂಡು ಹಿಡಿಯಿರಿ.

ಹಂತ 6: ಮಾನಕ ವಿಚಲನೆ ಕಂಡು ಹಿಡಿಯಿರಿ.:  () =  [(f*d²)/N]

 

5.5 ಉದಾ. 3: ಒಂದು ಪರೀಕ್ಷೆಯಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳು ಗಳಿಸಿದ ಅಂಕಗಳು ಹೀಗಿವೆ:-

 

ಅಂಕಗಳು	ಆವೃತ್ತಿ (f)	ಮಧ್ಯ ಬಿಂದು (x)	f*x	d=(X-)	d2	f*d2
25-30	5	28	140	-9.2	84.64	423.2
30-35	10	33	330	-4.2	17.64	176.4
35-40	25	38	950	0.8	0.64	16
40-45	8	43	344	5.8	33.64	269.12
45-50	2	48	96	10.8	116.64	233.28
	N = = 50		=1860			(f*d2)=1118

 

ವಿಧಾನ:

ಅಂಕಗಣಿತದ ಸರಾಸರಿ == /N = 1860/50 = 37.2

 

 

ಮಾನಕ ವಿಚಲನೆ: () =  [(f*d²)/N] =  (1118/50) =  (22.36) =4.728

 

ತೀರ್ಮಾನ: ವಿದ್ಯಾರ್ಥಿಗಳ ಅಂಕಗಳ ಸರಾಸರಿ =37.2. ವಿದ್ಯಾರ್ಥಿಗಳ ಅಂಕಗಳು ಸರಾಸರಿಯಿಂದ 5 ವಿಚಲನೆ ಹೊಂದುತ್ತವೆ.

 

ಪರ್ಯಾಯ ವಿಧಾನ (ಹಂತ - ವಿಚಲನಾಕ್ರಮ) [Alternate Method (Step – Deviation Method)]:

 

ಹಂತ 1: ದತ್ತಾಂಶಗಳಲ್ಲಿ ಸಾಧಾರಣ ಮಧ್ಯದಲ್ಲಿರುವ ಮೌಲ್ಯವನ್ನು ಸರಾಸರಿ ಎಂದಿಟ್ಟುಕೊಳ್ಳಿ (A).

 

ಹಂತ 2: ಊಹಿಸಿಕೊಂಡ ಸರಾಸರಿಯಿಂದ ‘ಹಂತ-ವಿಚಲನೆ’ (=d) ಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ:

d=(X-A)/i: ‘i’ ವರ್ಗಾಂತರದ ಗಾತ್ರ.

 

ಹಂತ 3: d², f*d ಮತ್ತು f*d² ಗಳನ್ನು ಪ್ರತಿ ವರ್ಗಾಂತರಕ್ಕು ಕಂಡುಹಿಡಿಯಿರಿ.

 

ಹಂತ 4: ಅಂಕಗಣಿತದ ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಗಳನ್ನು ಕೆಳಗಿನ ಸೂತ್ರದಂತೆ ಲೆಕ್ಕಹಾಕಿ.

ಅಂಕಗಣಿತದ ಸರಾಸರಿ: == A + [/N]*i 

 

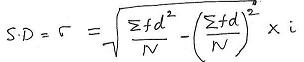
ಮಾನಕ ವಿಚಲನೆ: () =  [(f*d²)/N - ((f*d)/N)²]*i

 

ಮೇಲಿನ ಉದಾಹರಣೆ ಲೆಕ್ಕವನ್ನು ಈ ವಿಧಾನದಲ್ಲಿ ಮಾಡುವಾ.

ಅಲ್ಲಿ 43 ನ್ನ ಅಂದಾಜು ಸರಾಸರಿ (A) ಎಂದು ಊಹಿಸುವಾ.

i = ವರ್ಗಾಂತರದ ಗಾತ್ರ = 5.

ಹಂತ 1 ರಿಂದ 3 ರ ರೀತ್ಯಾ:

 

ಅಂಕಗಳು	ಆವೃತ್ತಿ (f)	ಮಧ್ಯ ಬಿಂದು (x)	d=(X-A)/i	f*d	d2	f*d2
25-30	5	28	-3	-15	9	45
30-35	10	33	-2	-20	4	40
35-40	25	38	-1	-25	1	25
40-45	8	43	0	0	0	0
45-50	2	48	1	2	1	2
	N = = 50			= - 58		(f*d2)=112

 

ಅಂಕಗಣಿತದ ಸರಾಸರಿ == A+ [/N]*i = 43 + [(-58/50)*5] = 43 + (-1.16)*5 = 43-5.8 = 37.2

ಮಾನಕ ವಿಚಲನೆ:

() =  [(f*d²)/N - ((f*d)/N)²]*i

=  [(112/50)- {-58/50} ²]*5

=  [2.24 - {-1.16} ²]*5

=  [2.24 – 1.3456]*5

=  [0.8944]*5

=.9457*5

=4.728

 

ತೀರ್ಮಾನ: ವಿದ್ಯಾರ್ಥಿಗಳು ಗಳಿಸಿದ ಅಂಕಗಳ ಸರಾಸರಿ = 37.2. ಅವರು ಗಳಿಸಿದ ಅಂಕಗಳು ಸರಾಸರಿಯಿಂದ 5 ಅಂಕಗಳಷ್ಟು ವಿಚಲಿತವಾಗುತ್ತವೆ.

 

ಸಾಮಾನ್ಯವಾಗಿ ವ್ಯಕ್ತಿಗಳ ತಂಡಗಳ ಸಾಧನೆಯನ್ನು ಹೋಲಿಸುವಾಗ ಅವರ ಸ್ಥಿರತೆಯ ಬಗ್ಗೆ ಮಾತನಾಡುತ್ತೇವೆ. ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರದಲ್ಲಿ ಈ ‘ಸ್ಥಿರತೆ’ಯನ್ನು ಹೇಗೆ ಗುರುತಿಸಬಹುದು?

 

ಈ ಸ್ಥಿರತೆಯನ್ನು ಲೆಕ್ಕ ಮಾಡಲು “ಮಾರ್ಪಿನ ಗುಣಾಂಕ” (Co efficient of variation) ವನ್ನು ಬಳಸುತ್ತೇವೆ. ಇದು ಹರವಿನ ಒಂದು ಸಾಪೇಕ್ಷ ಅಳತೆಯಾಗಿದೆ. ಇದನ್ನು ಈ ಕೆಳಗಿನ ಸೂತ್ರದಿಂದ ಲೆಕ್ಕ ಹಾಕುತ್ತೇವೆ.

ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾರ್ಪಿನ ಗುಣಾಂಕ *100/ ಸರಾಸರಿ.

 

ಆದ್ದರಿಂದ ಮಾರ್ಪಿನ ಗುಣಾಂಕವು ಮೂಲಮಾನಗಳಿಂದ ಮುಕ್ತವಾದ ಒಂದು ಸಂಖ್ಯೆ. ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಶೇಕಡಾ ರೂಪದಲ್ಲಿ ಸೂಚಿಸಲಾಗುವುದು. ಶೇಕಡಾ ಪ್ರಮಾಣ ಕಡಿಮೆಯಾದಷ್ಟು ಸ್ಥಿರತೆ ಹೆಚ್ಚು. ಸರಾಸರಿಗೆ ಹೋಲಿಸಿದಾಗ ಮಾನಕ ವಿಚಲನೆಯು ಚಿಕ್ಕ ಸಂಖ್ಯೆಯಾದರೆ, ಮಾರ್ಪಿನ ಗುಣಾಂಕ ಕಡಿಮೆಯಾಗುತ್ತದೆ.

 

ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ,

ಮಾರ್ಪಿನ ಗುಣಾಂಕ = (4.728*100)/37.2  =12.68

 

5.5 ಉದಾ. 4: A ಮತ್ತು B  ಎಂಬ ಇಬ್ಬರು ಕ್ರಿಕೆಟ್ ಆಟಗಾರರು 6 ಇನಿಂಗ್ಸ್‍ಗಳಲ್ಲಿ ಗಳಿಸಿದ ರನ್ನುಗಳು ಹೀಗಿದೆ:-

 

 

A ಆಟಗಾರ	48	50	54	46	48	54
B ಆಟಗಾರ	46	44	43	46	45	46

 

ಈ ಮೇಲಿನ ಇಬ್ಬರಲ್ಲಿ ಯಾರು ಉತ್ತಮ ಸ್ಕೋರರ್? ಯಾರು ಹೆಚ್ಚು ಸ್ಥಿರತೆ ಹೊಂದಿದ್ದಾರೆ?

 

ವಿಧಾನ:

 

ಈ ಇಬ್ಬರ ಸ್ಥಿರತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಲು ಮಾರ್ಪಿನ ಗುಣಾಂಕ ಕಂಡುಹಿಡಿಯಬೇಕು.

 

ಉದಾ. (5.1) ರಲ್ಲಿ ಈ A ಆಟಗಾರರ ರನ್ನುಗಳ ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಯನ್ನು ಲೆಕ್ಕ ಮಾಡಿದ್ದೇವೆ.

ಅಂಕಗಣಿತ ಸರಾಸರಿ = 50

ಮಾನಕ ವಿಚಲನೆ = 3.05

 ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾರ್ಪಿನ ಗುಣಾಂಕ *100/ ಸರಾಸರಿ = 3.05*100/50 = 6.1%

ಈಗ B ಆಟಗಾರನ ಸರಾಸರಿ ಮತ್ತು ಮಾರ್ಪಿನ ಗುಣಾಂಕ ಕಂಡುಹಿಡಿಯುವಾ.

 

 ಸರಾಸರಿ = 270/6 = 45

 

ಸಂ.	ರನ್ನುಗಳು (X)	ವಿಚಲನೆ (D) d= X-	d2
1	46	1	1
2	44	-1	1
3	43	-2	4
4	46	1	1
5	45	0	0
6	46	1	1
	=270	=0	=8

 

 

ಮಾನಕ ವಿಚಲನೆ,

 =  (/N)=  (8/6) = (1.33) = 1.15

 

 ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾನಕ ವಿಚಲನೆ *100/ ಸರಾಸರಿ = 1.15*100/45 =2.55%

 

ಫಲಿತಾಂಶ:

1. Aಯ ಸರಾಸರಿಯು B ಗಿಂತ ಹೆಚ್ಚು (50>45) ಆದ್ದರಿಂದ A ಯು B ಗಿಂತ ಉತ್ತಮ ಸ್ಕೋರರ್.

2. B ಯ ಮಾರ್ಪಿನ ಗುಣಾಂಕ  A ಗಿಂತ ಕಡಿಮೆ  (1.15<6.1) ಆದ್ದರಿಂದ B ಯು  ಹೆಚ್ಚು ಸ್ಥಿರ ಆಟಗಾರ.

 

5.5 ಉದಾ. 5: ಒಂದು ಪರೀಕ್ಷೆಯಲ್ಲಿ 10ನೇ ತರಗತಿಯ A ಮತ್ತು B ವಿಭಾಗದ ವಿದ್ಯಾರ್ಥಿಗಳು ಗಳಿಸಿದ ಅಂಕಗಳು ಹೀಗಿವೆ:-

 

ಅಂಕಗಳು	A  ವಿಭಾಗದ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ	B ವಿಭಾಗದ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ
25-30	5	5
30-35	10	12
35-40	25	20
40-45	8	8
45-50	2	5

 

 

ಯಾವ ವಿಭಾಗದ ಸಾಧನೆ ಉತ್ತಮವಾಗಿದೆ? ಯಾವ ವಿಭಾಗದ ಸಾಧನೆ ಹೆಚ್ಚು ಅಸ್ಥಿರ? ಈ ಸಮಸ್ಯೆ ಬಿಡಿಸಲು, ಅಂಕಗಣಿತ ಸರಾಸರಿ ಮತ್ತು ಮಾರ್ಪಿನ ಗುಣಾಂಕ ಬೇಕು.

 

5.5. ರ ಉದಾಹರಣೆ 3 ರಲ್ಲಿ A ವಿಭಾಗದ ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಗಳನ್ನು ಲೆಕ್ಕ ಮಾಡಿದ್ದೇವೆ.

 

ಅಂಕಗಣಿತದ ಸರಾಸರಿ =37.2

ಮಾನಕ ವಿಚಲನೆ=4.728

 

 ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾನಕ ವಿಚಲನೆ *100/ಸರಾಸರಿ = 4.728*100/37.2 =12.7%

ಈಗ B ಭಾಗಕ್ಕೆ ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಯನ್ನು ‘ಹಂತ-ವಿಚಲನ’ ಕ್ರಮದಲ್ಲಿ ಕಂಡುಹಿಡಿಯುವಾ.

ಹಂತ 1: ಅಂದಾಜಿನ ಸರಾಸರಿ: A =38 ಆಗಿರಲಿ. (A=28,33,43,48 ಯಾವುದೂ ಆಗಬಹುದು)

 

ಹಂತ 2: ಅಂದಾಜಿನ ಸರಾಸರಿಯಿಂದ ಹಂತ ವಿಚಲನೆಯನ್ನು (d) ಲೆಕ್ಕಹಾಕಿ.

 d=(X-A)/i: ‘i’  ವರ್ಗಾಂತರದ ಗಾತ್ರ = 5.

 

ಹಂತ 3: ಪ್ರತೀ ವರ್ಗಾಂತರಕ್ಕೂ d², f*d, f*d² ಕಂಡುಹಿಡಿಯಿರಿ.

 

ಹಂತ 4: ಸರಾಸರಿ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಲೆಕ್ಕ ಹಾಕಿ.

ಅಂಕಗಣಿತದ ಸರಾಸರಿ =  = A+ [/N]*i 

 

ಮಾನಕ ವಿಚಲನೆ = () =  [ (fd²)/N- { (fd)/N} ²]*i:

 

ಅಂಕಗಳು	ಆವೃತ್ತಿ (f)	ಮಧ್ಯ ಬಿಂದು (x)	d=(X-A)/i	fd	d2	fd2
25-30	5	28	-2	-10	4	20
30-35	12	33	-1	-12	1	12
35-40	20	38	0	0	0	0
40-45	8	43	1	8	1	8
45-50	5	48	2	10	4	20
	N = = 50			= - 4		(fd2)=60

 

ಅಂಕಗಣಿತ ಸರಾಸರಿ =  = A+ [()/N]*i 

    = 38 +[(-4/50)*5]

    = 38+ -0.08*5 = 43-0.4  = 37.6

ಮಾನಕ ವಿಚಲನೆ () =  [(f*d²)/N - ((f*d)/N)²]*i

       =  [(60/50)- {-4/50} ²]*5

       =  [1.2 - {-0.08} ²]*5

       =  [1.2 – 0.0064]*5

       =  [1.1936]*5

       =1.0925*5 =5.4625

 ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾನಕ ವಿಚಲನೆ *100/ ಸರಾಸರಿ = 5.4625*100/37.6  = 14.52%

 

ತೀರ್ಮಾನ:

1. B ವಿಭಾಗದ ಸರಾಸರಿ ಅಂಕವು A ವಿಭಾಗಕ್ಕಿಂತ ಹೆಚ್ಚಿದೆ (37.6>37.2), ಆದ್ದರಿಂದ B ಯ ಸಾಧನೆ A ಗಿಂತ ಉತ್ತಮ.

2. B ಯ ಮಾರ್ಪಿನ ಗುಣಾಂಕವು A ವಿಭಾಗಕ್ಕಿಂತ ಹೆಚ್ಚಿದೆ (14.52>12.7), ಆದ್ದರಿಂದ B ಯ ಸಾಧನೆಯು A ವಿಭಾಗಕ್ಕಿಂತ ಹೆಚ್ಚು ಅಸ್ಥಿರ.

 

5.5 ಉದಾ. 6: ಒಂದು ಕೈಗಾರಿಕಾ ಪ್ರದೇಶದಲ್ಲಿ A ಮತ್ತು B ಗಳೆಂಬ ಎರಡು ಕಾರ್ಖಾನೆಗಳಲ್ಲಿ ಕೊಡುವ ಸರಾಸರಿ ವಾರದ ವೇತನ ಮತ್ತು ಮಾನಕ ವಿಚಲನೆ ಹೀಗಿದೆ:-

ಕಾರ್ಖಾನೆ	ಸರಾಸರಿ ವೇತನ (ರೂ.ಗಳಲ್ಲಿ)	ವೇತನ ಮಾನಕ ವಿಚಲನೆ (ರೂ.)
A	34.5	6.21
B	28.5	4.56

 

ಯಾವ ಕಾರ್ಖಾನೆಯಲ್ಲಿ ವೇತನದಲ್ಲಿ ಹೆಚ್ಚು ತಾರತಮ್ಯವಿದೆ?

 

ವಿಧಾನ:

ಈಗ ನಾವು ಮಾರ್ಪಿನ ಗುಣಾಂಕವನ್ನು ಕಂಡು ಹಿಡಿಯಬೇಕು.

A ಕಾರ್ಖಾನೆಯ ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾನಕ ವಿಚಲನೆ *100/ಸರಾಸರಿ = 6.21*100/34.5 = 18%

B ಕಾರ್ಖಾನೆಯ ಮಾರ್ಪಿನ ಗುಣಾಂಕ = ಮಾನಕ ವಿಚಲನೆ *100/ಸರಾಸರಿ = 4.56*100/28.5 = 16%

A ಕಾರ್ಖಾನೆಯ ಮಾರ್ಪಿನ ಗುಣಾಂಕವು B ಕಾರ್ಖಾನೆಯ ದರಕ್ಕಿಂತ ಹೆಚ್ಚು (18>16). ಆದ್ದರಿಂದ A ಕಾರ್ಖಾನೆಯಲ್ಲಿ ವೇತನದಲ್ಲಿ ಹೆಚ್ಚು ತಾರತಮ್ಯವಿದೆ.

(A ಕಾರ್ಖಾನೆಯಲ್ಲಿ ನೌಕರಿಗೆ ಹೆಚ್ಚು ವೇತನವನ್ನು ಕೊಟ್ಟರೂ ಸಹ, ಅವರ ವೇತನಗಳಲ್ಲಿ ಹೆಚ್ಚು ತಾರತಮ್ಯವಿದೆ. )

 

5.5 ಕಲಿತ ಸಾರಾಂಶ

 

X = ಪ್ರಾಪ್ತಾಂಕಗಳ ಗಣ

 = ಅಂಕಗಣಿತದ ಸರಾಸರಿ (AM)

d = ಸರಾಸರಿಯಿಂದ ವಿಚಲನೆ.

f = ಮೌಲ್ಯಗಳ ಆವೃತ್ತಿ.

i = ವರ್ಗಾಂತರದ ಗಾತ್ರ.

x= ವರ್ಗಾಂತರದ ಮಧ್ಯ ಬಿಂದು.

 

 

ಸಂ.	ಸಂದರ್ಭ	ಆಯ್ಕೆ	N=	AM=	ವಿಚಲನೆ (d)	ಮಾನಕ ವಿಚಲನೆ ()
1	ಬಿಡಿ ಮೌಲ್ಯಗಳು		ಪ್ರಾಪ್ತಾಂಕಗಳ ಸಂಖ್ಯೆ	=()/N	X-
		A = ಯಾವುದೇ ಪ್ರಾಪ್ತಾಂಕ	ಪ್ರಾಪ್ತಾಂಕಗಳ ಸಂಖ್ಯೆ	= A+ ()/N	X-A
2	ಆವರ್ತ ಇರುವ ಮೌಲ್ಯಗಳು			=/N	X-
		A = ಯಾವುದೇ ಪ್ರಾಪ್ತಾಂಕ		= A + /N	X-A
3	ಆವರ್ತ ಇರುವ ವರ್ಗಾಂತರ			= /N	X-
		A = ಯಾವುದೇ ಪ್ರಾಪ್ತಾಂಕ		= A+ [/N]*i	d=(X-A)/i

 

ಸೂಚನೆ:ಮಾನಕ ವಿಚಲನೆಗೆ ಯಾವಾಗಲೂ ಸಾಮಾನ್ಯ ಸೂತ್ರ ನೆನಪಿಡಿ:-

 

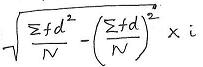
ವರ್ಗೀಕರಣ ಮಾಡದೇ ಇರುವ/ಆವರ್ತ ಇಲ್ಲದೇ ಇರುವ ಸಂದರ್ಭದಲ್ಲಿ, f=1, i=1 ಆದೇಶಿಸಿ, ಸಮಸ್ಯೆಗೆ ಸರಿಯಾದ ಸೂತ್ರ ಪಡೆಯಿರಿ

ಯಾವುದೇ ಮೌಲ್ಯವನ್ನು ಅಂದಾಜು ಸರಾಸರಿಯಾಗಿ ತೆಗೆದುಕೊಳ್ಳದಿದ್ದಾಗ, =0